Morrow method

In: local elastic-plastic strain methods->uniaxial methods

In comparison to the Feltner method, the emphasis in the Morrow parameter is placed on the energy closed in the hysteresis loop - the elastic part, which is again released during unloading, is not evaluated. The calculation of the energy in the hysteresis loop is based on the likelihood between cyclic deformation curve and the segment of the hysteresis loop (Massing rule):

The energy is not the same as a double of the Feltner's plastic part of his parameter as it should be - it contains the coeffiecient (1-n'), which is not in the Feltner's parameter. The exponent n' of the Ramberg-Osgood curve is replaced by the ratio of b and c exponents (see e-N curve) - beware that if you set it value directly in PragTic, the ratio of those two exponents b and c will be still used instead. The stress and plastic strain amplitudes are related to Basquin and Manson-Coffin curves:

.

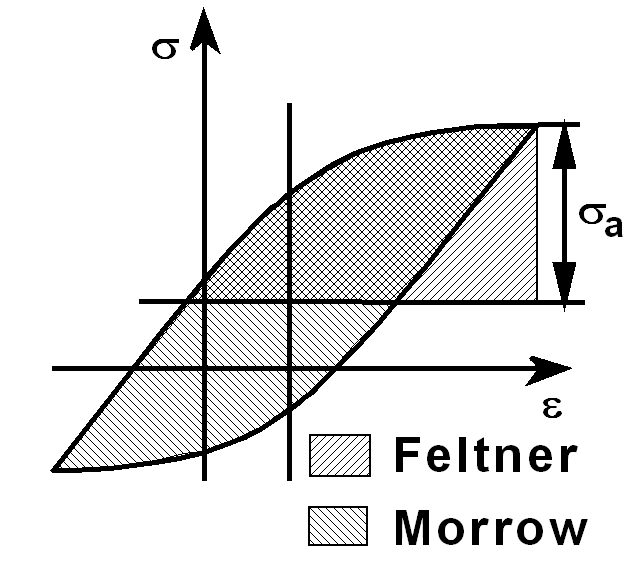
Fig.: Feltner method analysis is based on the energy applied during loading, while the Morrow parameter is related to the energy closed in the hysteresis loop.

The Morrow criterion in the original form lacks any adjustment to mean stress effect. The SWT correction for computation of the equivalent stress is therefore applied to all stress amplitudes in the previous formula:

Negative mean stress is expected to be non-damaging and its value is reset to zero. The conversion to an equivalent value allows a use of the common uniaxial rain-flow decomposition. The choice of the appropriate decomposition method is the point in Calculation Methods window, where the way of the tensor's reduction is chosen.

Nomenclature:

Decomposition

- Rain-flow with von Mises reduction

- Rain-flow with Tresca reduction

- Rain-flow with von Mises (signed) reduction

Elasto-plasticity

- No

- Neuber elastic-plastic accommodation

- Glinka elastic-plastic accommodation

Material parameters

© PragTic, 2007

This help file has been generated by the freeware version of HelpNDoc